A aceleración é unha magnitude física vectorial que mide a variación da velocidade respecto á variación do tempo. Descrito en termos diferenciais, dada unha función da posición dun móbil respecto ó tempo, a aceleración será a segunda derivada desta función respecto á variable temporal.

No contexto da mecánica vectorial newtoniana represéntase normalmente como a→displaystyle vec a, ou adisplaystyle mathbf a , e o seu módulo como adisplaystyle a,. As súas dimensións son [L⋅T−2]displaystyle scriptstyle [Lcdot T^-2]. Mídese en m/s² no Sistema Internacional.

Na mecánica newtoniana, para un corpo con masa constante, a aceleración do corpo é proporcional á forza que actúa sobre o mesmo (segunda lei de Newton):

F=ma→a=Fmdisplaystyle mathbf F =mmathbf a quad to quad mathbf a =cfrac mathbf F m

onde F é a forza resultante que actúa sobre o corpo, m é a masa do corpo, e a é a aceleración. A relación anterior é válida en calquera sistema de referencia inercial.

Introdución |

En conformidade coa mecánica newtoniana, unha partícula non pode seguir unha traxectoria curva a menos que sobre ela actúe unha certa aceleración, como consecuencia da acción dunha forza, xa que se esta non existise, o seu movemento sería rectilíneo. Así mesmo, unha partícula en movemento rectilíneo só pode cambiar a súa velocidade baixo a acción dunha aceleración na mesma dirección da súa velocidade (dirixida no mesmo sentido se acelera; ou en sentido contrario se desacelera).

Algúns exemplos do concepto de aceleración serían:

• A chamada aceleración da gravidade na Terra é a aceleración que produce a forza gravitatoria terrestre. O seu valor na superficie da Terra é, aproximadamente, de 9,8 m/s². Isto quere dicir que se se deixara caer libremente un obxecto, aumentaría a súa velocidade de caída a razón de 9,8 m/s por cada segundo (sempre que omitamos a resistencia aerodinámica do aire). O obxecto caería, polo tanto, cada vez máis rápido, respondendo dita velocidade a ecuación:

v=at=gt=9,8tdisplaystyle v=at=gt=9,8,t

• Unha manobra de freado dun vehículo, que se correspondería cunha aceleración de signo negativo, ou desaceleración, ao opoñerse á velocidade que xa tiña o vehículo. Se o vehículo adquirise máis velocidade, dito efecto chamaríase aceleración e, neste caso, sería de signo positivo.

Aceleración media e instantánea |

Definición da aceleración dunha partícula nun movemento calquera. Obsérvese que a aceleración non é tanxente á traxectoria.

Cada instante, ou sexa, en cada punto da traxectoria, queda definido un vector velocidade que, en xeral, cambia tanto en módulo como en dirección ao pasar dun punto a outro da traxectoria. A dirección da velocidade cambiará debido a que a velocidade é tanxente á traxectoria e esta, polo xeral, non é rectilínea. Na Figura represéntanse os vectores velocidade correspondentes aos instantes t e t+Δt, cando a partícula pasa polos puntos P e Q, respectivamente. O cambio vectorial na velocidade da partícula durante ese intervalo de tempo está indicado por Δv, no triángulo vectorial ao pé da figura. Defínese a aceleración media da partícula, no intervalo de tempo Δt, como o cociente:

<a>=a¯=ΔvΔtdisplaystyle <mathbf a >=mathbf bar a =frac Delta mathbf v Delta t

que é un vector paralelo a Δv e dependerá da duración do intervalo de tempo Δt considerado. A aceleración instantánea defínese como o límite ao que tende o cociente incremental Δv/Δt cando Δt→0; isto é, a derivada do vector velocidade con respecto ao tempo:

a=limΔt→0ΔvΔt=dvdtdisplaystyle mathbf a =lim _Delta tto 0frac Delta mathbf v Delta t=frac dmathbf v dt

Posto que a velocidade instantánea v á súa vez é a derivada do vector posición r respecto ao tempo, a aceleración é a derivada segunda da posición con respecto do tempo:

a=d2rdt2displaystyle mathbf a =frac d^2mathbf r dt^2

De igual forma pódese definir a velocidade instantánea a partir da aceleración como:

v−v0=∫t0t(dvdt)dtdisplaystyle mathbf v -mathbf v _0=int _t_0^tleft(mathrm d mathbf v over mathrm d tright),mathrm d t

Pódese obter a velocidade a partir da aceleración mediante integración:

v=∫0tadt+v0displaystyle mathbf v =int _0^tmathbf a dt+mathbf v _0

Medición da aceleración |

A medida da aceleración pode facerse cun sistema de adquisición de datos e un simple acelerómetro. Os acelerómetros electrónicos son fabricados para medir a aceleración nunha, dúas ou tres direccións. Contan con dous elementos condutivos, separados por un material que varia a súa condutividade en función das medidas, que á súa vez serán relativas á aceleración do conxunto.

Unidades |

As unidades da aceleración son:

• Sistema Internacional

1 m/s²

• Sistema Ceguesimal

1 cm/s² = 1 Gal

Compoñentes intrínsecos da aceleración: aceleración tanxencial e aceleración normal |

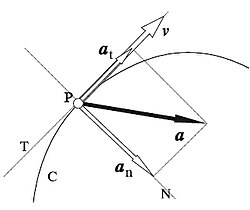
Compoñentes intrínsecos da aceleración.

En tanto que o vector velocidade v é tanxente á traxectoria, o vector aceleración a pode descompoñerse en dous compoñentes (chamados compoñentes intrínsecos) mutuamente perpendiculares: un compoñente tanxencial a_t (na dirección da tanxente á traxectoria), chamado aceleración tanxencial, e un compoñente normal a_n (na dirección da normal principal á traxectoria), chamado aceleración normal ou centrípeta (este último nome en razón a que sempre está dirixida cara ao centro de curvatura).

Derivando a velocidade con respecto ao tempo, tendo en conta que o vector tanxente cambia de dirección ao pasar dun punto a outro da traxectoria (isto é, non é constante) obtemos

a=dvdt=ddt(ve^t)=dvdte^t+vde^tdt=ate^t+v(ω×e^t)displaystyle mathbf a =frac dmathbf v dt=frac ddt(v,mathbf hat e _t)=frac dvdtmathbf hat e _t+vfrac dmathbf hat e _tdt=a_tmathbf hat e _t+v(boldsymbol omega times mathbf hat e _textt)

sendo e^tdisplaystyle mathbf hat e _t o vector unitario tanxente á traxectoria na mesma dirección que a velocidade e ωdisplaystyle boldsymbol omega a velocidade angular. Resulta conveniente escribir a expresión anterior na forma

a=dvdt=ate^t+v2ρe^n=ate^t+ane^ndisplaystyle mathbf a =frac dmathbf v dt=a_tmathbf hat e _t+frac v^2rho mathbf hat e _n=a_tmathbf hat e _t+a_nmathbf hat e _textn

sendo

e^ndisplaystyle mathbf hat e _n o vector unitario normal á traxectoria, isto é, dirixido cara ao centro de curvatura da mesma,

ρdisplaystyle rho , o raio de curvatura da traxectoria, isto é, o raio da circunferencia osculatriz á traxectoria.

As magnitudes destes dous compoñentes da aceleración son:

at=dvdtan=v2ρdisplaystyle a_t=frac dvdtqquad qquad qquad a_n=frac v^2rho

Cada un destes dous compoñentes da aceleración ten un significado físico ben definido. Cando unha partícula se move, a súa velocidade pode cambiar e este cambio mídeo a aceleración tanxencial. Pero se a traxectoria é curva tamén cambia a dirección da velocidade e este cambio mídeo a aceleración normal.

• Se no movemento curvilíneo a velocidade é constante (v=cte), a aceleración tanxencial será nula, pero haberá unha certa aceleración normal, de modo que nun movemento curvilíneo sempre haberá aceleración.


• Se o movemento é circular, entón o raio de curvatura é o raio R da circunferencia e a aceleración normal escríbese como a_n = v²/R.


• Se a traxectoria é rectilínea, entón o raio de curvatura é infinito (ρ→∞) de modo que a_n=0 (non hai cambio na dirección da velocidade) e a aceleración tanxencial a_t será nula ou non segundo a velocidade sexa ou non constante.

Os vectores que aparecen nas expresións anteriores son os vectores do triedro de Frênet que aparece na xeometría diferencial de curvas do seguinte xeito:

e^tdisplaystyle mathbf hat e _t é o vector unitario tanxente á curva.

e^ndisplaystyle mathbf hat e _n é o vector unitario normal á curva.

ωdisplaystyle boldsymbol omega é o vector velocidade angular que é paralelo ao vector binormal á curva.

Movemento circular uniforme |

Cinemática do movemento circular.

Un movemento circular uniforme é aquel no que a partícula percorre unha traxectoria circular de raio R con velocidade constante, é dicir, que a distancia percorrida en cada intervalo de tempo igual é a mesma. Para ese tipo de movemento o vector de velocidade mantén o seu módulo e vai variando a dirección seguindo unha traxectoria circular. Se se aplican as fórmulas anteriores, tense que a aceleración tanxencial é nula e a aceleración normal é constante: esta aceleración normal chámase "aceleración centrípeta". Neste tipo de movemento a aceleración simplemente modifica a traxectoria do obxecto e non a súa velocidade.

a=dvdt=dvdte^t+v2Re^n=0⋅e^t+v2Re^n=ω2R e^ndisplaystyle mathbf a =frac dmathbf v dt=frac dvdtmathbf hat e _t+frac v^2Rmathbf hat e _n=0cdot mathbf hat e _t+frac v^2Rhat mathbf e _n=omega ^2R hat mathbf e _n

Movemento rectilíneo acelerado |

No Movemento Rectilíneo Acelerado, a aceleración instantánea queda representada como a pendente da recta tanxente á curva que representa graficamente a función v(t).

Se se aplican as fórmulas anteriores ao movemento rectilíneo, no que só existe aceleración tanxencial, ao estar todos os vectores contidos na traxectoria, podemos prescindir da notación vectorial e escribir simplemente:

a=dvdtdisplaystyle a=frac dvdt

Xa que nese tipo de movemento os vectores adisplaystyle scriptstyle mathbf a e vdisplaystyle scriptstyle mathbf v son paralelos, satisfacendo tamén a relación:

v(t)=v0+∫0ta(τ) dτdisplaystyle v(t)=v_0+int _0^ta(tau ) dtau

As coordenadas de posición veñen dada neste caso por:

x(t)=x0+v0t+∫0t(t−τ)a(τ) dτdisplaystyle x(t)=x_0+v_0t+int _0^t(t-tau )a(tau ) dtau

Un caso particular de movemento rectilíneo acelerado é o movemento rectilíneo uniformemente acelerado, onde a aceleración é ademais constante e polo tanto, a velocidade e as coordenadas de posición veñen dadas por:

v(t)=v0+at,x(t)=x0+v0t+at22displaystyle v(t)=v_0+at,qquad x(t)=x_0+v_0t+frac at^22

Aceleración en mecánica relativista |

O análogo da aceleración en mecánica relativista chámase cuadriaceleración e é un cuadrivector cuns tres compoñentes espaciais que para pequenas velocidades coinciden cos da aceleración newtoniana (o compoñente temporal para pequenas velocidades resulta proporcional á potencia da forza divida pola velocidade da luz e a masa da partícula).

En mecánica relativista a cuadrivelocidade e a cuadriaceleración son sempre ortogonais, iso vén de que a cuadrivelocidade ten un (pseudo)módulo constante:

U⋅U=c2 ⇒ 2U⋅dUdτ=0 ⇒ 2U⋅A=0displaystyle mathbf U cdot mathbf U =c^2 Rightarrow 2mathbf U cdot frac dmathbf U dtau =0 Rightarrow 2mathbf U cdot mathbf A =0

onde c é a velocidade da luz e o produto anterior é o produto asociado á métrica de Minkowski:

V⋅W:=η(V,W)=ημνVμVνdisplaystyle Vcdot W:=eta (V,W)=eta _mu nu V^mu V^nu

Véxase tamén |

Wikimedia Commons ten máis contidos multimedia na categoría:  Aceleración

Bibliografía |

• 
  Serway, Raymond A.; Jewett, John W. (2004). Brooks/Cole, ed. Physics for Scientists and Engineers (6ª ed.). ISBN 0-534-40842-7. 
  


• 
  Tipler, Paul (2004). Physics for Scientists and Engineers: Mechanics, Oscillations and Waves, Thermodynamics (5ª ed.). W. H. Freeman. ISBN 0-7167-0809-4. 
  


• 
  Ortega, Manuel R. (1989-2006). Monytex, ed. Lecciones de Física (4 volumes) (en español). ISBN 84-404-4290-4, ISBN 84-398-9218-7, ISBN 84-398-9219-5, ISBN 84-604-4445-7. 
  


• 
  Resnick,Robert & Krane, Kenneth S. (2001). John Wiley & Sons, ed. Physics (en inglés). New York. ISBN 0-471-32057-9. 
  


• 
  Tipler, Paul A. (2000). Barcelona: Ed. Reverté, ed. Física para la ciencia y la tecnología (2 volumes) (en español). ISBN 84-291-4382-3. 
  

Ligazóns externas |

• 
  Serie de vídeos explicativos sobre a aceleración en caída libre no YouTube (en castelán)
  


• 
  Acceleration and free fall - a chapter from an online textbook (en inglés)


• 
  Science aid: Movement (en inglés)
  


• 
  Science.dirbix: Acceleration (en inglés)
  


• 
  Acceleration Calculator (en inglés)