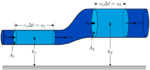
Sistema mecánico no cal consérvase a enerxía, para choque perfectamente elástico e ausencia de atrito.

A lei de conservación da enerxía establece que o valor da enerxía dun sistema illado (sen interacción con ningún outro sistema) permanece invariable co tempo. A conservación da enerxía dun sistema está ligada ao feito de que as ecuacións de evolución sexan independentes do instante considerado.

En termodinámica, constitúe o primeiro principio da termodinámica. En mecánica analítica, pode demostrarse que o principio de conservación da enerxía é unha consecuencia de que a dinámica de evolución dos sistemas está rexida polas mesmas características en cada instante do tempo. Iso conduce a que a "traslación" temporal sexa unha simetría que deixa invariante as ecuacións de evolución do sistema, polo que o teorema de Noether leva a que existe unha magnitude conservada, a enerxía.

Conservación da enerxía e termodinámica |

Dentro dos sistemas termodinámicos, unha consecuencia da lei de conservación da enerxía é a chamada Primeira lei da termodinámica, que establece que, dada unha cantidade de enerxía térmica Q que flúe dentro dun sistema, debe aparecer como un incremento da enerxía interna (ΔU) do sistema ou como un traballo (W) efectuado polo sistema sobre os seus arredores:

ΔU= Q+ Wdisplaystyle Delta U= Q+ W

Aínda que a enerxía non se perde, degrádase. Hai formas de enerxía que se poden transformar ou aproveitar mellor. Ó final e tras sucesivas conversións a enerxía acaba en forma de calor. Esta calor é moi difícil de converter noutras enerxías, polo menos cun rendemento próximo ó rendemento do ciclo de Carnot, e, ademais, necesítase unha diferenza de temperatura. Moitas veces non se pode aproveitar e hai que descartar o seu uso. Ás veces, fai falta enerxía extra para desfacerse del.
Desde un punto de vista cotián, as máquinas e os procesos desenvolvidos polo ser humano funcionan cun rendemento menor que o 100%, o que se traduce en "perdas de enerxía" medido en términos económicos ou materiais, sen que isto deba interpretarse como un non cumprimento do principio enunciado.

O principio en mecánica clásica |

En mecánica lagranxiana a conservación da enerxía é unha consecuencia do teorema de Noether cando o lagranxiano non depende explicitamente do tempo. O teorema de Noether asegura que cando se ten un lagranxiano independente do tempo, e polo tanto, existe un grupo uniparamétrico de traslacións temporais ou simetría, pode construírse unha magnitude formada a partir do lagranxiano que permanece constante ao longo da evolución temporal do sistema, esa magnitude coñécese como hamiltoniano do sistema. Se ademais a enerxía cinética é unha función só do cadrado das velocidades xeralizadas (ou o que é equivalente a que os vínculos no sistema sexan esclerónomos, é dicir, independentes do tiempo), pode demostrarse que o hamiltoniano nese caso coincide coa enerxía mecánica do sistema, que en tal caso se conserva.

En mecánica newtoniana o principio de conservación da enerxía, non pode derivarse dun principio tan elegante como o teorema de Noether, pero pode comprobarse directamente para certos sistemas simples de partículas no caso de que todas as forzas deriven dun potencial, o caso máis sinxelo é o dun sistema de partículas puntuais que interactúan a distancia de modo instantáneo.

O principio en mecánica relativista |

Unha primeira dificultade para xeneralizar a lei de conservación da enerxía da mecánica clásica á teoría da relatividade está en que en mecánica relativista non se pode distinguir adecuadamente entre masa e enerxía. Así, de acordo con esta teoría, a presenza dunha partícula material de masa m en repouso respecto dun observador implica que devandito observador medirá unha cantidade de enerxía asociadada a ela dada por E = mc². Outro feito experimental contrastado é que na teoría da relatividade non é posible formular unha lei de conservación da masa análoga á que existe en mecánica clásica, xa que esta non se conserva. Así, aínda que na mecánica relativista non existan leis de conservación separadas para a enerxía non asociada á masa e para a masa, non obstante, si é posible formular unha lei de conservación "masa-enerxía" ou enerxía total.

Dentro da teoría da relatividade especial, a materia pode representarse como un conxunto de campos materiais a partir dos que se forma o chamado tensor de enerxía-impulso total e a lei de conservación da enerxía exprésase en relatividade especial, empregando o convenio de sumación de Einstein, na forma:

(1)
∂Tαβ∂xβ=∂Tα0∂x0+∂Tα1∂x1+∂Tα2∂x2+∂Tα3∂x3=0displaystyle frac partial T^alpha beta partial x^beta =frac partial T^alpha 0partial x^0+frac partial T^alpha 1partial x^1+frac partial T^alpha 2partial x^2+frac partial T^alpha 3partial x^3=0

A partir desta forma diferencial da conservación da enerxía, dadas as propiedades especias do espazo-tempo na teoría da relatividade especial sempre conduce a unha lei de conservación en forma integral. Esa integral representa precisamente unha mangitude física que permanece invariable ao longo da evolución do sistema e é precisamente a enerxía. A partir da expresión (1), escrita en termos de coordenadas galileanas (x0=ct,x1=x,x2=y,x3=z)displaystyle (x^0=ct,x^1=x,x^2=y,x^3=z);, e empregando o teorema da diverxencia tense:

(2)
1cddt∫Ti0dV=−∮⁡TiαdSαdisplaystyle frac 1cfrac ddtint T^i0,dV=-oint T^ialpha ,dS_alpha

Se a segunda integral que representa o fluxo de enerxía e momento linear se anula, como sucede por exemplo se se estende a integral a todo o espazo-tempo para un sistema illado chégase á conclusión de que o primeiro membro da expresión anterior permanece invariable durante o tempo. É dicir:

(3)
ddtPi=0,Pi:=1c∫Ti0dVdisplaystyle frac ddtP^i=0,qquad P^i:=frac 1cint T^i0,dV

A compoñente "temporal" E=cP00displaystyle E=cP^00, é precisamente a enerxía total do sistema, sendo as outras tres as compoñentes do momento linear nas tres direccións espaciais.

Conservación en presenza de campo electromagnético |

En presenza de campos electromagnéticos a enerxía cinética total das partículas cargadas non se conserva. Por outra banda aos campos eléctrico e magnético, polo feito de seren entidades físicas que cambian en relación ao tempo segundo a dinámica propia dun lagranxiano, pode asignárseles unha magnitude chamada enerxía electromagnética dada por unha suma de cadrados do módulo de ambos os campos que satisfai:

(4)
∂∂t(ε0E2+B2μ0)+∂Ecin∂t=0displaystyle frac partial partial tleft(varepsilon _0mathbf E ^2+frac mathbf B ^2mu _0right)+frac partial E_cinpartial t=0

O termo dentro da primeira paréntese é a integral estendida a todo o espazo da compoñente T00displaystyle T^00, que de acordo coa sección precedente debe ser unha magnitude conservada para un campo electromagnético adecuadamente confinado.

Conservación en presenza de campo gravitatorio |

Debido ás peculiaridades do campo gravitatorio, tal como se trata dentro desta teoría, non existe unha maneira de construír unha magnitude que represente a enerxía total conxunta da materia e o espazo-tiempo que se conserve. A explicación intuitiva deste feito é que debido a que un espazo-tempo pode carecer de simetría temporal, feito que se reflicte en que non existen vectores de Killing temporais en devandito espazo, non pode falarse invariancia temporal das ecuacións de movemento, ao non existir un tempo alleo ao propio tempo coordenado do espazo-tempo.

Outra das consecuencias do tratamento que fai a teoría da relatividade xeral do espazo-tiempo é que non existe un tensor de enerxía-impulso ben definido. Aínda que para certos sistemas de coordenadas pode construírse o chamado pseudotensor de enerxía-impulso, con propiedades similares a un suspensorio, pero que só pode definirse en sistemas de coordenadas que cumpren certas propiedades específicas.

Por outra banda, mesmo na teoría da relatividade xeral para certo tipo de sistemas moi especiais, pode construírse unha magnitude asimilable á enerxía total do sistema. Un exemplo destes sistemas son os espazo-tempos asintoticamente planos caracterizados por unha estrutura causal peculiar e certas condicións técnicas moi restritivas; estes sistemas son o equivalente en teoría da relatividade dos sistemas illados.

Finalmente cómpre sinalar, que dentro dalgunhas teorías alternativas á relatividade xeral, como a teoría relativista da gravitación de Logunov e Mestvirishvili, si pode definirse univocamente a enerxía total do sistema de materia. Esta teoría é totalmente equivalente á teoría da relatividade xeral en rexións desprovistas de materia, e predí desviacións da mesma só en rexións ocupadas por materia. En particular, a teoría de Logunov e Mestvirishvili, predí a non ocorrencia de buratos negros,^[1] e esa é unha das principais predicións que a diferencian da teoría xeral da relatividade de Albert Einstein.

O principio en mecánica cuántica |

Na mecánica cuántica aparece así a enerxía total en certos sistemas illados non está fixada para algúns estados cuánticos senón que pode flutuar ao longo do tempo. Só os estados chamados estacionarios que son autovectores do operador hamiltoniano teñen unha enerxía ben definida, cando ademais o hamiltoniano non depende do tempo.

Porén, en sistemas illados aínda para estados non estacionarios, pode definirse unha lei de conservación da enerxía en termos de valores medios. De feito, para un sistema cuántico calquera o valor medio da enerxía dun estado puro vén dado por:

(1)
ddt⟨E⟩t=⟨Ψ(t)|∂H^∂t|Ψ(t)⟩displaystyle frac ddtlangle Erangle _t=langle Psi (t),

e polo tanto cando o hamiltoniano non depende do tempo, como sucede nun sistema illado o valor esperado da enerxía total consérvase. Aínda que para algúns estados se observen flutuacións oscilantes da enerxía cunha desviación típica que se relacionan co principio de indeterminación de Heisenberg mediante:

(2)
ΔE⋅Δt≥ℏ2displaystyle Delta Ecdot Delta tgeq frac hbar 2,

onde:
ΔE:=⟨Ψ(t)|H^2|Ψ(t)⟩−⟨E⟩2displaystyle Delta E:=sqrt hat H^2

Notas |

Véxase tamén |

Wikimedia Commons ten máis contidos multimedia na categoría:  Conservación da enerxía

Outros artigos |

• Criterio de signos termodinámico


• Termodinámica


• Enerxía


• Lei de conservación


• Criterio de signos termodinámico


• Física

v c e Mecánica de medios continuos Leis básicas Conservación da masa Conservación da enerxía Ecuacións de Navier-Stokes Mecánica de fluídos Fluído Tensión superficial Cantidade de movemento Mecánica de sólidos deformábeis Elasticidade Plasticidade Lei de Hooke